Binary Search Trees
Let’s consider a Linked List that we’ve seen so far for the problem of storing and retrieving information. In particular, let’s implement a set using an ordered linked list as the underlying data structure. Here’s how that would look like:

From the get-go we can see that searching and inserting would be slow for this implementation. Say we want to check if node E exists in the list or not. We’ll start searching at the begining of the list, perform a check to see if a node matches the key we’re searching for, and if not, move on to the next node in the list. This will lead to O(N) time complexity for search, which is definitely not good.
Note: The ideas and content (including images) in this post come from Josh Hug’s excellent lectures from UC Berkeley’s CS61B.
Slightly better than a List
Let’s try to analyze the problem. Even though we have a sorted list, we’re not able to make use of that property for searching. Let’s make a simple change here. Instead of having the sentinel node (of the list) point to A, let’s have it point to the node at the middle of the list, ie, D. And, let’s have the next linkages point outwards from D such that C points to B, which instead points to A, and the same for the right hand side. Here’s how that would look like:

This is a major upgrade! We can now make use of the fact that nodes to the left of D (ie, A, B, and C) will be smaller than D, whereas those in the right side of D will be larger than D. If we now search for E, we can simply skip the left side, and start searching the right side. Time taken to search is halved (on average)!
Let’s do even better
Let’s double down on this idea. Since the 3 nodes in each half are also in order, we can again split them up as 2 sides of the middle element. That is, we recursively do the same thing we did before, and go from the above representation to this:

which can be rearranged to look like this:
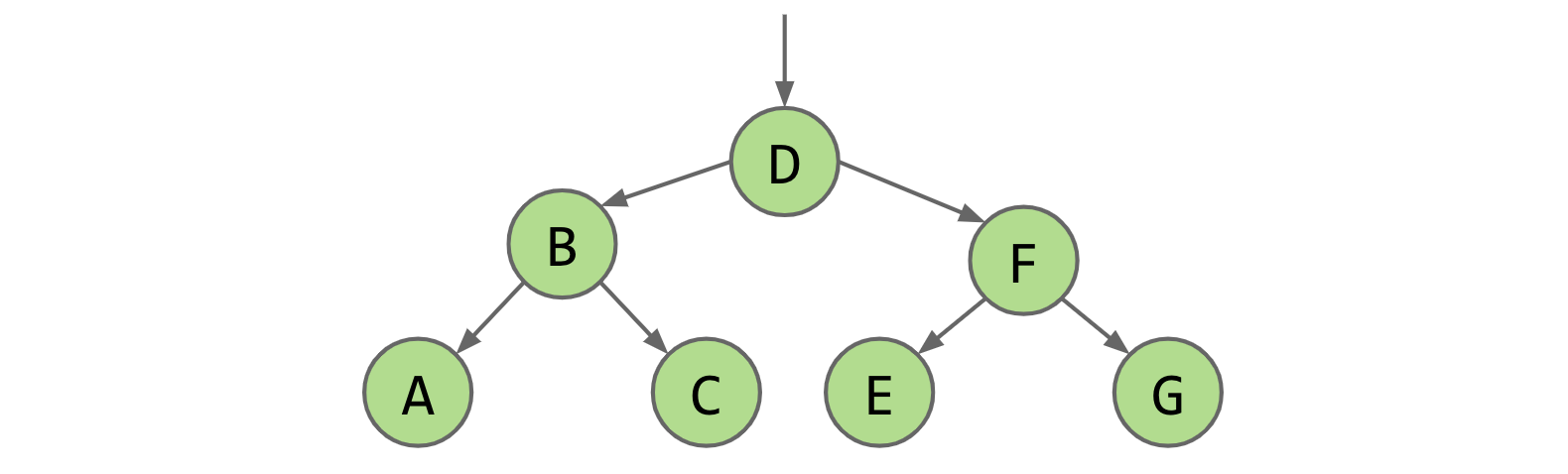
That’s it! This is a binary search tree. In order to get to E, we need to do 3 comparison checks (at E, F, and finally at E itself). Another point to note here is that the number of nodes at each level of the tree is double of that in the previous level. Hence, the number of nodes will have to double (to 16) in order to do 4 comparison checks (Technically, this is only true for bushy BSTs; we’ll get to this later). That is pretty sweet because it indicates logarithmic performance.
To summarize, for every node X in a BST:
- Every key in the left subtree is less than X’s key.
- Every key in the right subtree is greater than X’s key.
Implementation
Let’s try to understand the working of a BST by using it as the underlying data structure for a Map (let’s call it BSTMap), something which maps a key to a value. We’ll first see some pseudocode for an operation, and then see code specific for the Map implementation. The entire implementation can be found here.
First, we need to write the definition of a Node, which holds a single data point. A Node will have a key, a value, references to it’s left and right children (if any), and a size value. size will hold the number of nodes in the subtree with that particular node as it’s root.
private class Node {
private K key;
private V value;
private Node left, right;
private int size;
public Node(K key, V value, int size) {
this.key = key;
this.value = value;
this.size = size;
}
}
Next, let’s see how insert, search, and delete work in a BST.
Search
The pseudocode for searching a BST is really elegant and simple. We recursively call the search function based on whether the search key is less than or greater than the key of the node being compared to. In short,
If searchKey equals T.key, return.
- If searchKey ≺ T.key, search T.left.
- If searchKey ≻ T.key, search T.right.
/**
* Pseudo code for BST search
*/
static BST find(BST T, Key sk) {
if (T == null)
return null;
if (sk.equals(T.key))
return T;
else if (sk ≺ T.key)
return find(T.left, sk);
else
return find(T.right, sk);
}
Notes directly from the CS61B lecture:
Bushy BSTs are extremely fast. At 1 microsecond per operation, can find something from a tree of size 10^300000 in one second. Since a lot of computation is dedicated towards finding things in response to queries, it’s a good thing that we can do such queries almost for free.
Here’s the implementation code for search in BSTMap.
/**
* Private helper function for search
* in BSTMap
*/
private V get(Node x, K key) {
if (x == null) {
return null;
}
int cmp = key.compareTo(x.key);
if (cmp == 0) {
return x.value;
} else if (cmp < 0) {
return get(x.left, key);
} else {
return get(x.right, key);
}
}
Insert
Inserting a new node in a BST can be thought of as follows:
- Search for key.
- If found, do nothing.
- If not found:
- Create new node.
- Set appropriate link.
/**
* Pseudo code for insert in a BST
*/
static BST insert(BST T, Key ik) {
if (T == null)
return new BST(ik);
if (ik ≺ T.key)
T.left = insert(T.left, ik);
else if (ik ≻ T.key)
T.right = insert(T.right, ik);
return T;
}
There is some beautiful recursion going on here. At every level in the BST, based on whether the new key is less or greater than the node in consideration, we set the left or right reference to be the result of a recursive call to insert itself. Doing this will automatically place the new node at the correct place in the BST. Here’s the implementation for insert in BSTMap.
/**
* Helper function for insert in BSTMap
*/
private Node put(Node x, K key, V value) {
if (x == null) {
return new Node(key, value, 1);
}
int cmp = key.compareTo(x.key);
if (cmp < 0) {
x.left = put(x.left, key, value);
} else if (cmp > 0) {
x.right = put(x.right, key, value);
} else {
x.value = value;
}
x.size = x.size + 1;
return x;
}
Delete
Deletion is slightly more tricky than searching or inserting. Deletion of a node can fall under one of these three cirumstances:
- Deletion of a node with no children
- Deletion of a node with one child
- Deletion of a node with two children
Let’s consider these 3 cases one by one:
Delete node with no children
This is pretty simple case. We just sever the parent’s link to the node to be deleted. The removed node will be garbage collected.
delete “glut”
Delete node with one child
This is just a bit more complicated than the last one. Let’s consider the example of deleting the node with the key flat. In this case, since flat has only one child (elf), we can safely point dog’s child pointer — right, in this case — to elf whilst still maintaing BST property in the tree. On doing this, flat will be garbage collected.
delete “flat”
Delete node with 2 children
This is the trickiest of the 3 cases since we can’t just change left or right pointers in the tree and be done with it. We also need to replace the deleted node with some other node to maintain BST property after deletion. Let’s consider the case of deletion of dog in the following BST.
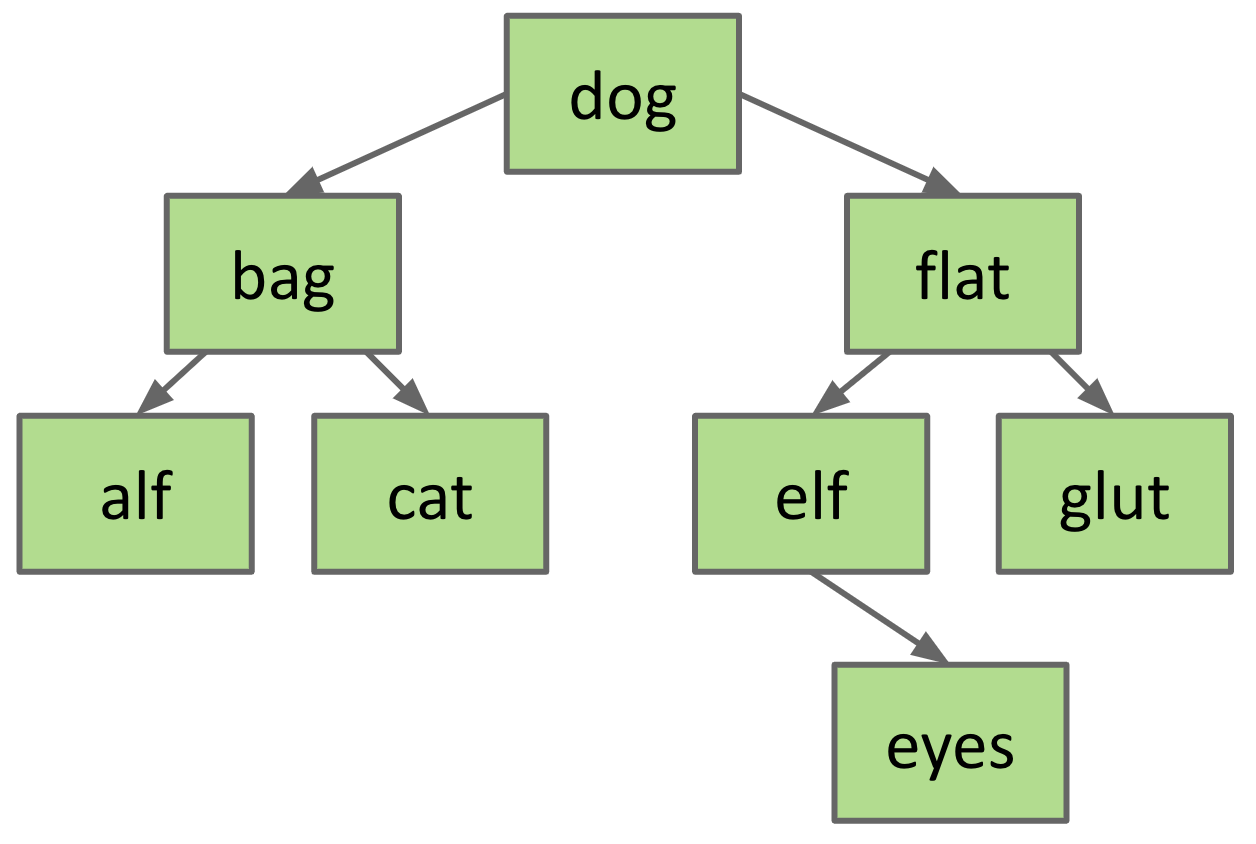
The node that replaces dog has to be greater than everything in the left subtree of dog, and it has to be less than everything in the right subtree of dog. We solve this problem by finding either a “successor” or a “predecessor” for dog. Let’s work with the “successor” for this example.
The “successor” of dog is defined as the first node in the right subtree of dog which has no left child. The “successor” of dog in this case is elf. Once we’ve found the “successor”, we simply replace dog’s key (and other properties) with those of elf.
Similarly, the “predecessor” of dog is the first node in the left subtree of dog which has no right child. In this case, it’s cat.
Note: The predecessor or successor is guaranteed to not have more than 1 children.
Delete “dog”
Here’s what the implementation for deleting a node looks like in BSTMap.
/**
* Helper function for deletion
*/
private Node remove(Node T, K key) {
int cmp = key.compareTo(T.key);
if (cmp < 0) {
T.left = remove(T.left, key);
} else if (cmp > 0) {
T.right = remove(T.right, key);
}
// we've found the node to be removed,
// now check if it has zero, one, or
// two children
else if (T.left == null) {
return T.right;
} else if (T.right == null) {
return T.left;
} else {
// remove node with two children
T.right = swapSmallest(T.right, T);
}
T.size -= 1;
return T;
}
/**
* Helper function for Hibbard deletion.
* Always finds successor.
*/
private Node swapSmallest(Node T, Node R) {
if (T.left == null) {
//change R's properties
R.key = T.key;
R.value = T.value;
return T.right;
} else {
T.left = swapSmallest(T.left, R);
T.size -= 1;
return T;
}
}
Symmetric vs Asymmetric Hibbard Deletion
There’s a fun little fact about random deletions from a Binary Search Tree. If we perform an experiment where we randomly delete a node from BST, then randomly insert a new node, and do this over and over, we see that the average depth of the tree first decreases, then continues to increase well above the starting depth.
A point to note here is that this is only the case with asymmetric Hibbard deletion, ie, the case where deleted nodes with two children are replaced only by a “successor” or a “predecessor”. If we change the deletion mechanism to randomly choose between a “successor” and a “predecessor”, we see that the average depth drops and continues to stay down over the course of deletions/insertions. This can be seen in the following experiments (part of CS61B’s Challenge Lab 7).

Average depth of a BST over multiple asymmetric deletions and insertions
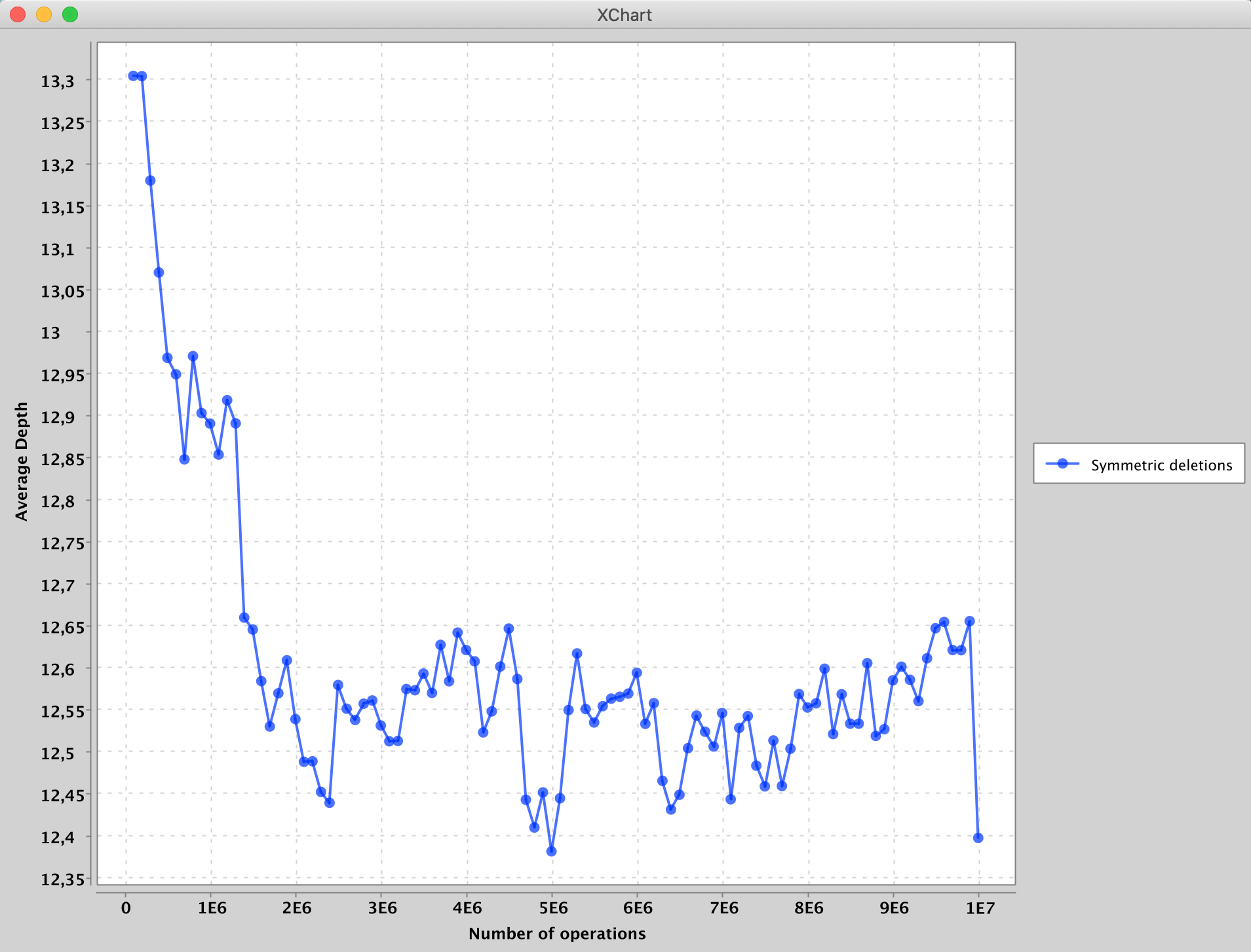
Average depth of a BST over multiple symmetric deletions and insertions
References
- Josh Hug’s lectures from CS61B.