Summary Notes: Forward and Back Propagation
I recently completed the first course offered by deeplearning.ai, and found it incredibly educational. Going forwards, I want to keep a summary of the stuff I learn (for my future reference) in the form of notes like this. This one is for forward and back-prop intuitions.
Setup
A neural network with $L$ layers.
Notation:
- $l$ ranges from 0 to $L$. Zero corresponds to input activations and $L$ corresponds to predictions.
- Activation of layer $l$: $a^{[l]}$
- Training examples are represented as column vectors. So X is of shape $(n^{[0]},m)$, where $n^{[0]}$ is number of input features.
- Weights for layer $l$ have shape: $(n^{[l]},n^{[l-1]})$
- Biases for layer $l$ have shape: $(n^{[l]},1)$
Forward Propagation Intuition (for batch gradient descent)
Forward prop will simply take in inputs from layer $a^{[l-1]}$, calculate linear and non-linear activations based on its weights and biases, and propagate them to the next layer.
For layer $l$, forward prop function:
Takes in inputs
- activations of previous layer: $a^{[l-1]}$
- weights for that layer: $w^{[l]}$
- biases for that layer: $b^{[l]}$
Calculates
- Linear activation of that layer: $z^{[l]}$
- Non-linear activation of that layer: $a^{[l]}$
Steps
- Calculate linear activation:
$$ \large z^{[l]} = w^{[l]}.a^{[l-1]} + b^{[l]} $$
- Calculate non-linear activation:
$$ \large a^{[l]} = g^{[l]}(z^{[l]})$$
(where $g^{[l]}$ is the activation function for that layer, eg. relu, tanh, sigmoid)
- Cache $a^{[l-1]}$, $w^{[l]}$, $b^{[l]}$, and $z^{[l]}$ (implementation detail, cache to be used by backpropagation)
- For output layer $a^{[L]} = \hat{y}$ (ie predictions)
Backpropagation Intuition (for batch gradient descent)
Back-prop calculates gradients of the parameters of each layer wrt to the cost function, moving from right to left.
For layer $l$, back-prop function:
Takes in inputs
- gradients of activations of the layer: $da^{[l]}$
- activations of previous layer: $a^{[l-1]}$ (from cache)
- weights for that layer: $w^{[l]}$ (from cache)
- biases for that layer: $b^{[l]}$ (from cache)
Calculates
- gradients of the linear activations for that layer: $dz^{[l]}$ (Used to calculate gradients of the below two)
- gradients of weights for that layer: $dw^{[l]}$
- gradients of biases for that layer: $db^{[l]}$
Steps
- Once forward prop is complete, calculate loss $\mathcal{L}$
- Derive $da^{[L]} = \frac{\partial \mathcal{L} }{\partial a^{[L]}}$ using the formula of Loss function. eg. In case of sigmoid activation,
$$ \large \mathcal{L} = -y\log\left(a^{[L]}\right) + (1-y)\log\left(1- a^{[L]}\right) $$ $$ \large da^{[L]} = -(\frac{y}{a^{[L]}} + \frac{(1-y)}{1- a^{[L]}}) $$
- Once you have $da^{[l]}$, compute
$$ \large dz^{[l]} = da^{[l]} * g’(z^{[l]})$$
(where $g^{[l]}$ is the activation function for that layer)
- Since $z^{[l]} = w^{[l]}.a^{[l-1]} + b^{[l]}$, gradients of $w^{[l]}$, $b^{[l]}$, and $a^{[l-1]}$ can now be calculated.
- Simple calculus derivatives result in:
$$ \large dw^{[l]} = \frac{\partial \mathcal{L} }{\partial z^{[l]}} . \frac{\partial z^{[l]}}{\partial w^{[l]}} = dz^{[l]} a^{[l-1]} $$
$$ \large db^{[l]} = \frac{\partial \mathcal{L} }{\partial z^{[l]}} . \frac{\partial z^{[l]}}{\partial b^{[l]}} = dz^{[l] (i)}$$
$$ \large da^{[l-1]} = \frac{\partial \mathcal{L} }{\partial z^{[l]}} . \frac{\partial z^{[l]}}{\partial a^{[l-1]}} = w^{[l]} dz^{[l]} $$
- $dw^{[l]}$ and $db^{[l]}$ are the gradients of the parameters of the neural network, whereas $da^{[l-1]}$ is required to continue backpropagation.
- This process is repeated till we reach the first layer.
Summary in simple words
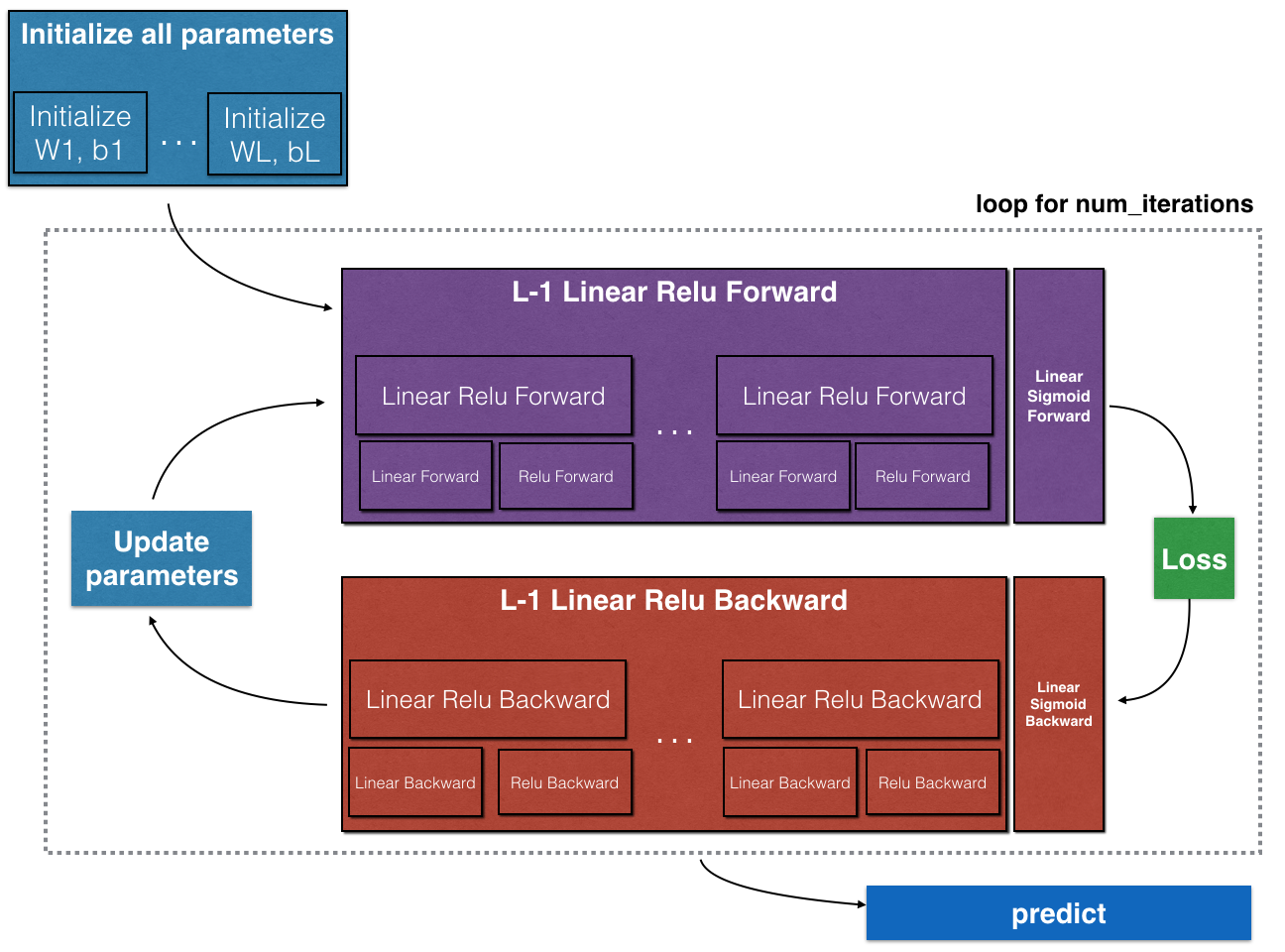
Start from the input layer and compute activations for each layer. At the last layer, the activation(s) will be the predictions of the neural network. Compute loss. Calculate gradients of the linear activations for each layer, which will then be used to calculate gradients of weights and biases for each layer. Update the parameters after each such walkthrough.