Understanding the A star algorithm

I recently learnt about the workings of the A* algorithm through Udacity’s Intro to Self Driving Cars Nanodegree, and wanted to understand it in detail, hence this post on it.

Wikipedia article on A* states: “A star is a computer algorithm that is widely used in pathfinding and graph traversal, which is the process of finding a path between multiple points, called “nodes”. It enjoys widespread use due to its performance and accuracy.”

It was devised by Peter Hart, Nils Nilsson and Bertram Raphael of Stanford Research Institute (now SRI International) who first published the algorithm in 1968.

Setup

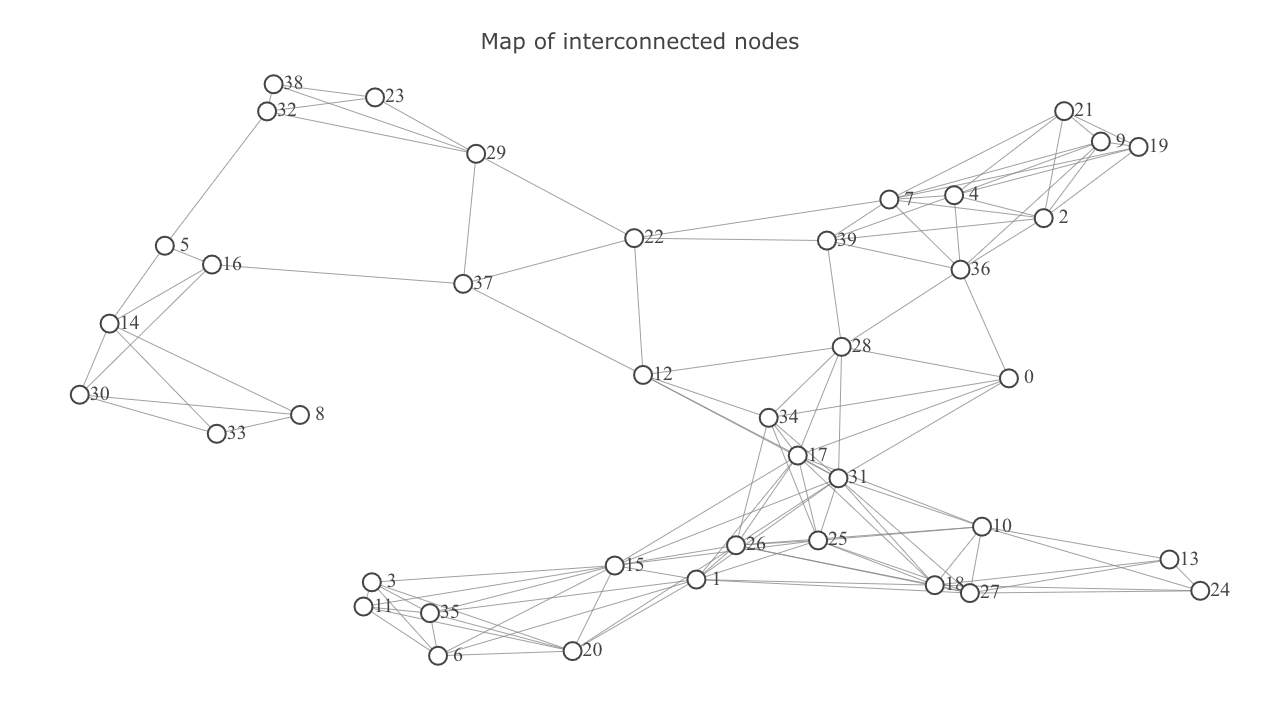
We have a map of interconnected nodes and the problem that we want to solve is to find the shortest path between two nodes.

Terminology

Let’s define some terminology that will help us understand the algorithm.

• Initial state ($s_0$) in the case of route finding refers to being at a starting node.
• Actions $(s)$ -> ${a_1,a_2,a_3,…}$ It refers to producing outcomes for a particular state. eg. the possible actions for the state of being at node 8 are movement to nodes 14, 30, and 33.
• Result $(s,a)$ -> $s’$ The combination of being in a particular state and taking a particular action produces a new state. eg. the state of being at node 8 and action of moving to node 14 results in the state of being at node 14 with it’s own set of further possible actions.
• Step Cost refers to the cost incurred in taking an action. In the case of route finding, it can be the distance travelled while going from one node to another.
• Path Cost is the summation of individual step costs along a path consisting of one or more nodes.
• State Space is the set of all states we can be in. We navigate the state space by applying actions.

The A-star Algorithm

Let’s start understanding these concepts using the map shown above. Let’s use node 8 as start goal and node 2 as goal node.

A* uses a metric called f-score which is a score to gauge how fruitful moving to the neighbor will be in finding the optimal path. $$ f = g + h $$ where $f$ is the f-score, $g$ or g-score is the path cost of a node, and h is a heuristic used to estimate distance between a node and the goal. In this case, we’ll be using euclidian distance between two nodes as the heuristic.

Currently, the g-score of node 8 is zero while that of all others is set to infinity (as we don’t have that knowledge yet). As a result, the f-score of all nodes except 8 is infinity. f-score of 8 is just the value of $h$ for 8.

To make our lives easier we’ll divide up the state space into separate segments:

• Explored
• Frontier
• Unexplored

We’ll start with the frontier consisting just the start node. Until the frontier is empty or we reach the goal node, we’ll do the following:

• Choose the node with the lowest f-score. At this moment it’s node 8. Let’s call this node the current node.
• If the current node is the goal node, we’re done. If not, remove it from the frontier and add it to the explored set.
• Start exploring the neighbors of the current node. represents current node, and represents the neighbor being considered.

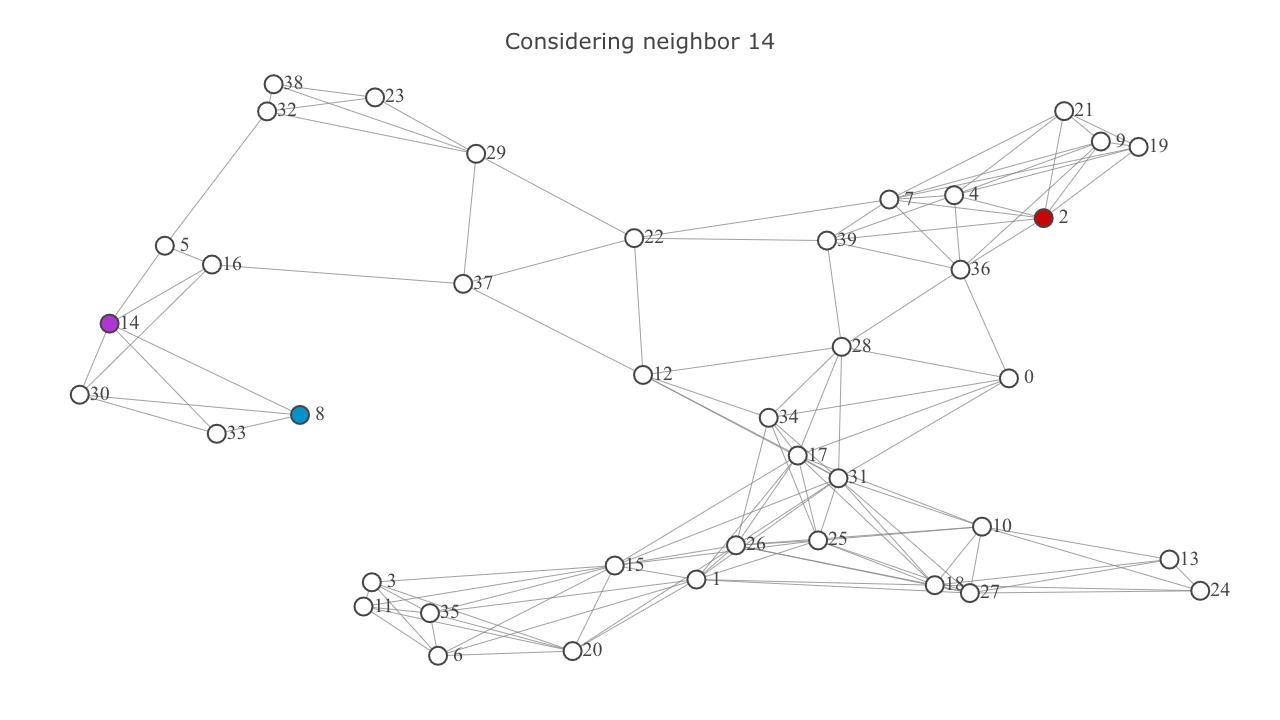
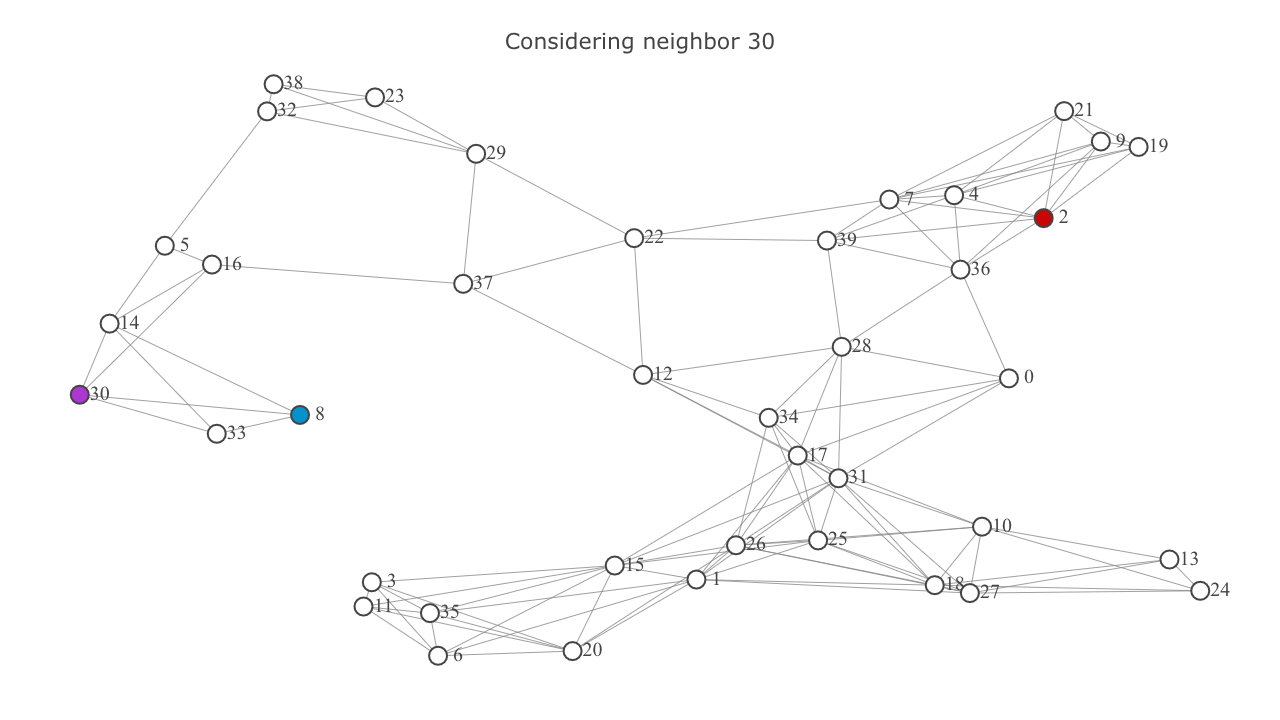
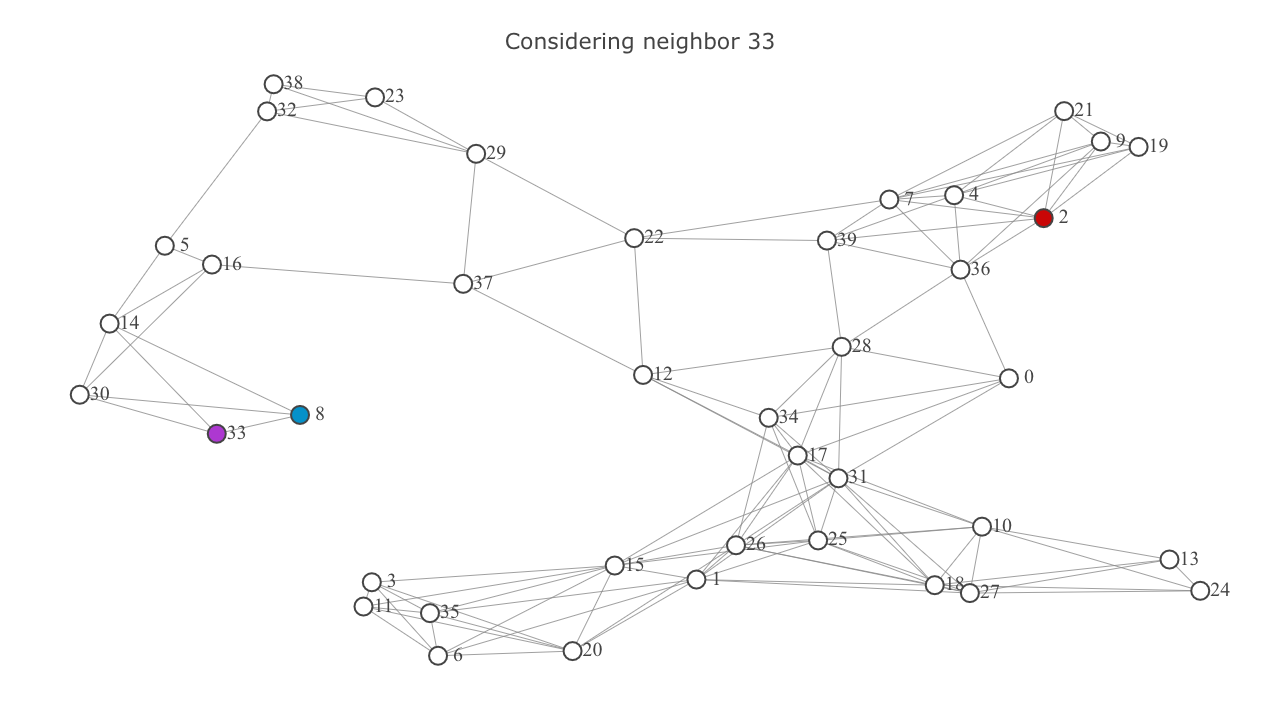
• Add each neighbor to the frontier if it’s not already in it. Ignore the neighbor if it’s in the explored set. This will be highlighted below in the video frames titled “Already explored: {node}”.
• In the former case (ie, if the neighbor wasn’t in the explored set), calculate it’s tentative g-score. In this case the tentative g-score is the sum of the g-score of current and the euclidian distance between current and the neighbor. Set the neighbor’s g-score as this tentative score. Also update the neighbor’s f-score.

This is how the map looks after one iteration of exploration. represents the frontier set.

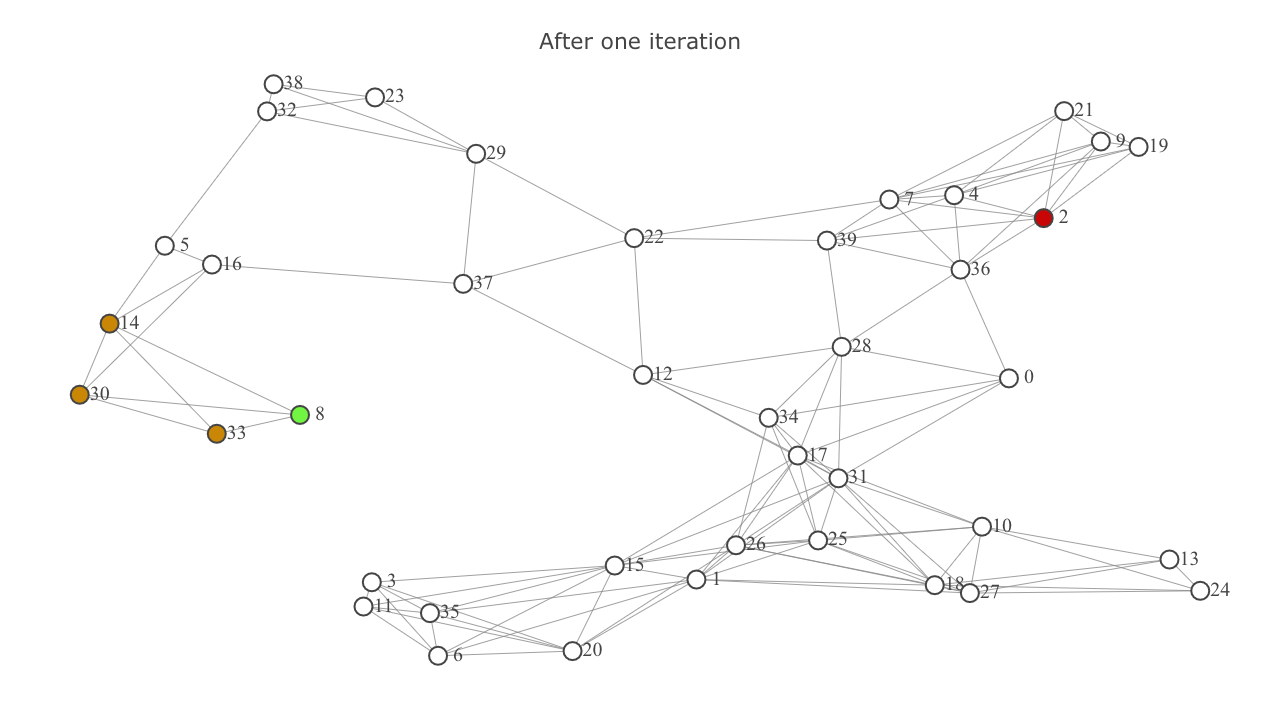
• Now we repeat the above steps again. This time the node with the lowest f-score will be 33.
• One point to take note here is that if the tentative g-score of a neighbor node is greater than or equal to it’s already calculated g-score, there exists a better route to the neighbor than the path being considered. This will be highlighted below in the video frames titled “Better route exists to: {node}”.

This is how the map looks after second iteration. The explored set is indicated by and includes the nodes 8 and 33. (8 is highlighted as since it’s the start node).

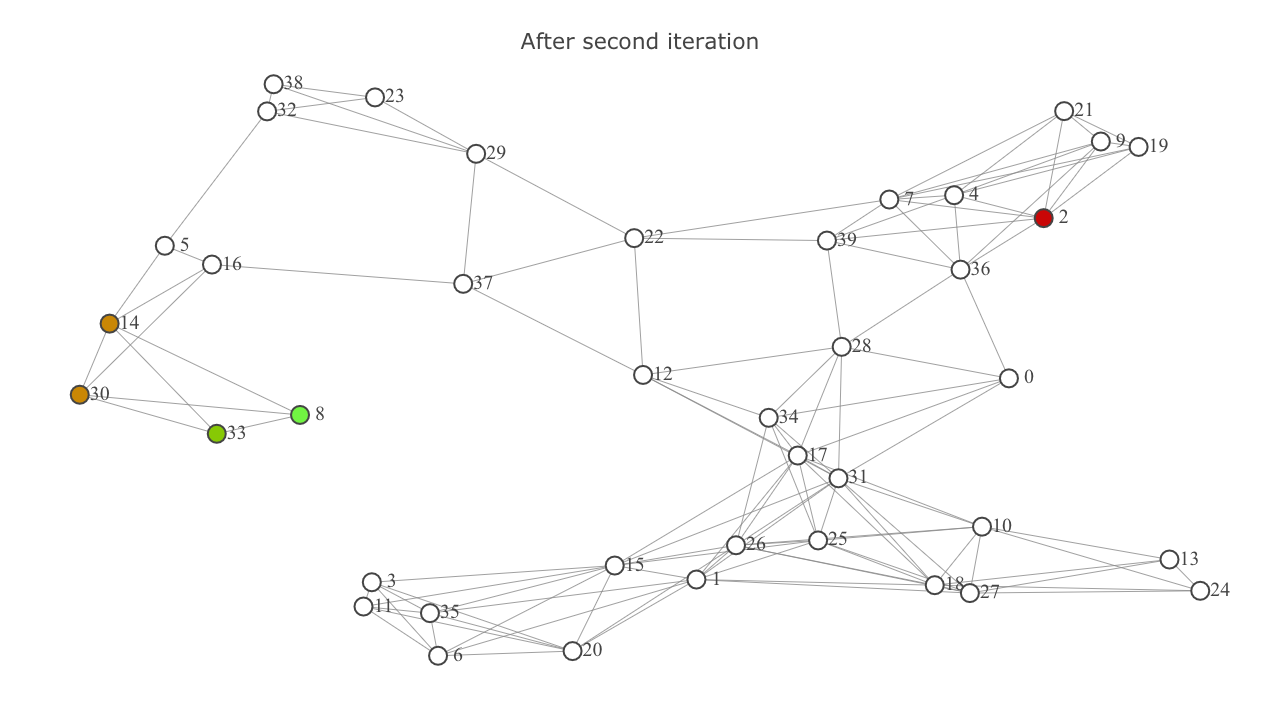
This is how things look after the third iteration.

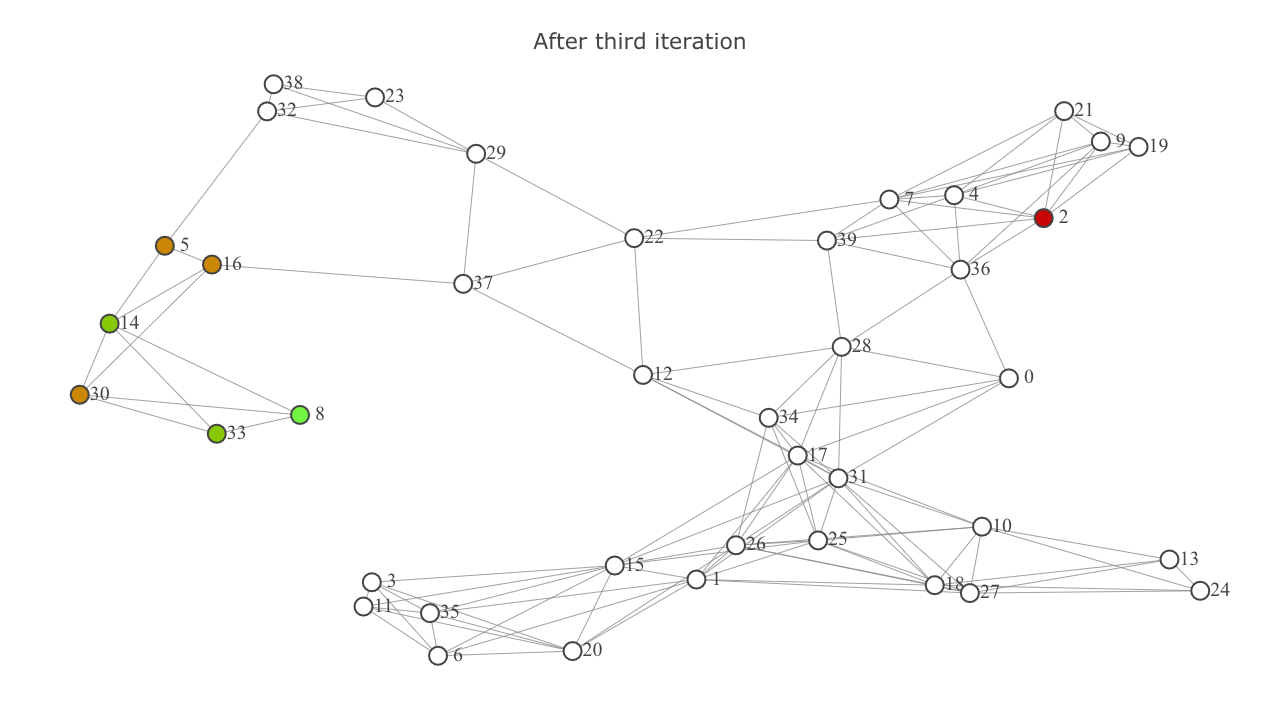
A-star summed up

• Start with the frontier consisting of a single node, which is the start node.
• Set up g-scores for all nodes to infinity except the start node, which is set to zero. As a result, f-scores for all nodes except the start node is also infinity.
• While there are nodes in the frontier, in each iteration, choose the node with the lowest f-score. Term it as current node for the current iteration.
• Go through each of this node’s neighbors, and update it’s g-score and f-score using the formula $f = g + h$ where $g$ is the path cost of the neighbor (from the start node), and $h$ is the heuristic. Ignore the neighbor if it’s already in the frontier or the explored set. Also ignore the neighbor if the tentative g-score of neighbor (g-score of “current node” + euclidian distance between “current node” and the neighbor) is greater than or equal to the g-score of the neighbor. (This means that there exists a shorter route to the neighbor than the current route being considered).
• Repeat last two steps until the current node is the goal node, or the frontier is empty.

Demo

Below is a video which shows the implementation of A* for finding shortest route between nodes 8 and 2.

represents the start node.
represents the goal node.
represents nodes in the frontier set.
represents nodes in the explored set.
represents current node, ie, the node with the lowest f-score.
represents neighbors of the current node being considered for exploration.

Shortest route between nodes 20 and 22:

Shortest route between nodes 38 and 21:

Code for the implementation can be found here.

References

• Intro to Self Driving Car ND
• Wikipedia page on A* algorithm